
What Do Efficiency Numbers Mean
The analysis of college basketball using the efficiency method produces three values, offensive efficiency, defensive efficiency and net game efficiency. The offensive efficiency is the number of points scored per possession and the defensive efficiency is the number of points allowed per possession. The net game efficiency is the offensive efficiency minus the defensive efficiency and indicates the average margin or victory [when positive] or loss [when negative].
It is clear that an individual possession can produce 0 to 4 points. The 1995-96 championship Kentucky team achieved an offensive efficiency for the entire season of approximately 0.96 ppp. Since 1995, I have not seen an offensive efficiency significantly higher that this level. FN1 Over the 2000, 2001 and 2002 seasons, the Kentucky average offensive efficiencies have been 0.84, 0.93 and 0.88 ppp. During the 2002 season, the average offensive efficiencies for ACC and SEC teams at the conclusion of the 2002 regular season was about 0.89 ppp. [Click Here To See Tabulation of All Kentucky Seasons Since 1972]
Similarly, the 1995-96 championship Kentucky team posted an average defensive efficiency of approximately 0.75. As with the offensive efficiency noted above for that championship team, I have not seen a defensive efficiency significantly lower than this level. FN2 Over the 2000, 2001 and 2002 seasons, the Kentucky average defensive efficiencies have been 0.78, 0.82 and 0.78 ppp. During the 2001-02 season, the ACC and SEC teams had an average defensive efficiency of about 0.82 ppp. [Click Here To See Tabulation of All Kentucky Seasons Since 1972]
The real key to a team's success over the course of a full season is a function of the net game efficiencies. 1995-96 championship Kentucky team posted an average net game efficiency of approximately 0.21 ppp. As with the offensive efficiency noted above for that championship team, I have not seen a net game efficiency significantly higher than this level. FN3 Over the 2000, 2001 and 2002 seasons, the Kentucky average net game efficiencies have been 0.065, 0.113, and 0.106 ppp. During the 2001-02 season, the ACC and SEC teams had an average net game efficiency of about 0.064 ppp. [Click Here To See Tabulation of All Kentucky Seasons Since 1972] FN4
The actual game to game efficiencies occur in a statistically significant pattern around these average efficiency values. The standard deviation of any particular distribution indicates the consistency of that team's play, either offensive and defensive. If the statistical distribution of offensive and defensive efficiencies are superimposed onto the same graph, we can visualize this relationship.
If a team's average offensive and defensive efficiencies are about equal, we can deduce that on any given game, that team is just as likely to perform better on offense as on defense, then should win about half of their games. Similarly, if a team's average offensive efficiency is a little higher than its defensive efficiency, e.g. a positive Net Game Efficiency, then that team is more likely to out perform its opponent on any particular game. It is intuitively obvious that as the Net Game Efficiency increases, the probability of winning a particular game increases. Of course, similar conclusions apply to teams with negative Net Game Efficiencies.
The overlapping areas of the offensive and defensive distributions speak to the probabilities. Clearly, the difference between the means is the Net Game Efficiency. When I consider these statistical distributions, I like to compare the portion of these distributions that overlap with the areas that do not overlap. The ratio of the overlapping area to the sum of both total areas is the probable winning or losing percentage. For example, if these data completely overlap, the team has equal probability of winning and losing when it plays. As the Net Game Efficiency increases [or decreases] from zero, the probability of winning or losing increase and decrease.
A team's winning percentage is a function of this difference. A statistically significant relationship exists between the net average game efficiency and the team's winning percentage. Teams with winning percentages of 50% +/- 4% have a difference between their offensive and defensive efficiencies near zero [-0.065 to 0.069]. Teams with a 65% to 75% winning percentage sport a value of about 0.059 to 0.115. Teams with an 80% to 90% winning percentage have a net game efficiency of about 0.120 to 0.208.
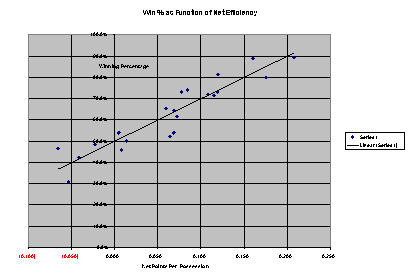
The attached graph illustrates this data and the trend line based on a linear regression analysis. Obviously, a linear relationship appears reasonable for this data within the range of values presented in this graph. However, in reality, a non-linear relationship must exist because the maximum winning percentage possible is 100% and the minimum is 0%. However, within the range of data presented, the following formula describes the relationship.
Winning Percentage = 0.50 +2*(Net Game Efficiency)
Valid when net game efficiency<0.25 OR > -0.10
Some may argue that the comparisons presented above are not valid because each season is a unique experience. Different teams appear on the schedule from one year to the next. In addition, the teams that appear each year on the schedule are not themselves the same quality one year to the next. I fully understand the point. These factors may influence the absolute values of offensive and defensive efficiencies; however, the net game efficiency should be free of these seasonal distortions. Furthermore, these year-to-year comparisons are only valid for season long performances when the cumulative quality of the schedule is comparable one year to the next. The former condition should be satisfied for teams in the major conferences.
This concern about the influence of the strength of schedule may be significant when comparing offensive and defensive efficiencies of two disparate teams. For example, comparing Kentucky or Florida results to Rider or Iona may yield similar absolute values when in reality, the quality of the competition overall was stronger for the former than the latter. However, this supposition may also be elitist.
An area of future study should consider the schedule strength as an independent variable. In this regard, beginning with the 2005 season, I will examine the relationship between average efficiencies and the RPI Strength of Schedule for the respective teams to determine whether I can identify an empirical algorithym that enables more reliable comparison of teams.
Absent this analysis, it would seem logical that the significance of this strength of schedule variations should be less important when comparing teams from the same or similar conferences. Teams from the same conference play a significant number of their season games against each other and common opponents.
When the efficiency is the principal guiding real time statistic, it becomes readily apparent that the keys to success in college basketball include the pace of the game, the percentage of possessions that end without a scoring opportunity, the efficiency achieved during the scoring opportunities, and the consistency of these factors over the course of a season.
Footnotes:
1. The 2001-02 Duke basketball team, on March 1, 2002 , has an average offensive efficiency of about 0.98 ppp.
2. The 2001-02 Duke basketball team, on March 1, 2002 , has an average defensive efficiency of about 0.77 ppp.
3. The 2001-02 Duke basketball team, on March 1, 2002 , has an average net game efficiency of about 0.21 ppp.
4. The Spread Sheet begins with the 1972 season because that ts the first season that Kentucky's Media Guide statistics include Turnovers. The 1972 season was Coach Rupp's last. Therefore, the data includes the full Hall, Sutton, Pitino and Smith tenures as Kentucky coach. I would like to draw the reader's attention to specific data in this table.
a) Net Game Efficiency v. Normalized Net Game Efficiency. The normalized values remove the affect of offensive rebounding differential, e.g. both teams have the same number of total possessions for the game. Note that the normalized values will be higher when the Kentucky team earns more offensive rebounds than its opponents.
b) Turnover Rate, Kentucky and Opponents, expressed as Possessions per Turnover. Obviously, the higher the value, the fewer turnovers committed. Note the following averages by coach:
Years Coach No. of Turnover Rate, Poss/TO
From - To
Name Seasons Kentucky Opponents
1972 - 1972 Rupp 1 6.46 6.02
1973 - 1986 Hall
14 5.74 5.88
1973 - 1979 Hall, #1 7 5.76 5.42
1979 - 1986 Hall #2 7 5.82 6.42
1987 - 1989 Sutton
3 5.83 5.29
1990 - 1997 Pitino 8 6.15 4.45
1998 - 2005 Smith 8 5.75 5.22
Totals 34 5.87 5.34
2004-05 Team Smith [ 09 Games] 7.05 3.82
Maximum Kentucky TO Rate, 1990 6.71
Minimum Kentucky TO Rate, 1983 5.07
Maximum Opponent TO Rate, 1981 8.69
Minimum Opponent TO Rate, 1997 3.88
Please note that the 2004-05 team is currently posting record breaking turnover rates, both in terms of protecting its possessions and forcing turnovers on defense.
c) For those who observe a significant difference above for Coach Hall's first 7 years and his second 7 years, I percieve similar differences in several important statistical categories. Over the last 34 years, Kentucky has consistently committed fewer turnovers than it forced. The glaring exception to this rule is the second 7 years of Coach Hall's tenure. Consider the data for Average Possessions per Game [Game Pace]:
Coach Hall Possessions Per Game
Tenure Kentucky Opponents
Hall #1 94.7 92.8 [Fastest Pace of coaches]
Hall #2 79.5 77.4 [Slowest Pace of coaches]
This invites the questions: Why did Coach Hall change his coaching philosophy following the 1979 season? Did the change of pace, from very fast to very slow cause the change in turnover rates?
Copyright 2004 Richard Cheeks
All Rights Reserved